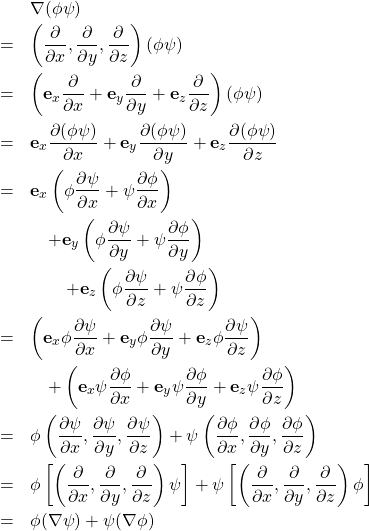ベクトル解析の公式の一覧

ベクトル解析の公式の一覧（ベクトルかいせきのこうしきのいちらん）では、3次元空間におけるベクトル解析の公式の一覧を与える。

内積と外積

ここで ${\displaystyle \mathbf {A} }$, ${\displaystyle \mathbf {B} }$, ${\displaystyle \mathbf {C} }$ は任意のベクトルである。また重複添え字については和を取る（アインシュタインの縮約記法）。${\displaystyle \epsilon _{ijk}}$ はレヴィ＝チヴィタ記号、${\displaystyle \theta }$ は ${\displaystyle \mathbf {A} }$, ${\displaystyle \mathbf {B} }$ がなす角である。

内積

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{i}B_{i}=A_{x}B_{x} A_{y}B_{y} A_{z}B_{z}=|\mathbf {A} ||\mathbf {B} |\cos \theta }$

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\mathbf {B} \cdot \mathbf {A} }$

外積

${\displaystyle \mathbf {A} \times \mathbf {B} =(\epsilon _{ijk}A_{j}B_{k})\mathbf {e} _{i}=(A_{y}B_{z}-A_{z}B_{y})\mathbf {e} _{x} (A_{z}B_{x}-A_{x}B_{z})\mathbf {e} _{y} (A_{x}B_{y}-A_{y}B_{x})\mathbf {e} _{z}}$

${\displaystyle \mathbf {A} \times \mathbf {B} =-\mathbf {B} \times \mathbf {A} }$

${\displaystyle |\mathbf {A} \times \mathbf {B} |=|\mathbf {A} |\mathbf {B} |\sin \theta }$

スカラー三重積

${\displaystyle \mathbf {A} \cdot (\mathbf {B} \times \mathbf {C} )=\mathbf {B} \cdot (\mathbf {C} \times \mathbf {A} )=\mathbf {C} \cdot (\mathbf {A} \times \mathbf {B} )}$

ベクトル三重積

${\displaystyle \mathbf {A} \times (\mathbf {B} \times \mathbf {C} )=(\mathbf {A} \cdot \mathbf {C} )\mathbf {B} -(\mathbf {A} \cdot \mathbf {B} )\mathbf {C} }$

ヤコビ恒等式

${\displaystyle \mathbf {A} \times (\mathbf {B} \times \mathbf {C} ) \mathbf {B} \times (\mathbf {C} \times \mathbf {A} ) \mathbf {C} \times (\mathbf {A} \times \mathbf {B} )=0}$

四重積

${\displaystyle (\mathbf {A} \times \mathbf {B} )\cdot (\mathbf {C} \times \mathbf {D} )=(\mathbf {A} \cdot \mathbf {C} )(\mathbf {B} \cdot \mathbf {D} )-(\mathbf {A} \cdot \mathbf {D} )(\mathbf {B} \cdot \mathbf {C} )}$

${\displaystyle (\mathbf {A} \times \mathbf {B} )\times (\mathbf {C} \times \mathbf {D} )=[\mathbf {A} \cdot (\mathbf {C} \times \mathbf {D} )]\mathbf {B} -[\mathbf {B} \cdot (\mathbf {C} \times \mathbf {D} )]\mathbf {A} }$

微分公式

ここで ${\displaystyle \mathbf {A} }$, ${\displaystyle \mathbf {B} }$ は任意のベクトル場, ${\displaystyle f}$ は任意のスカラー場である。

${\displaystyle \mathbf {\nabla } \cdot (f\mathbf {A} )=\mathbf {\nabla } f\cdot \mathbf {A} f\mathbf {\nabla } \cdot \mathbf {A} }$

${\displaystyle \mathbf {\nabla } (\mathbf {A} \cdot \mathbf {B} )=(\mathbf {B} \cdot \mathbf {\nabla } )\mathbf {A} (\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} \mathbf {A} \times (\mathbf {\nabla } \times \mathbf {B} ) \mathbf {B} \times (\mathbf {\nabla } \times \mathbf {A} )}$

${\displaystyle \mathbf {\nabla } \cdot (\mathbf {A} \times \mathbf {B} )=\mathbf {B} \cdot (\mathbf {\nabla } \times \mathbf {A} )-\mathbf {A} \cdot (\mathbf {\nabla } \times \mathbf {B} )}$

${\displaystyle \mathbf {\nabla } \times (f\mathbf {A} )=\mathbf {\nabla } f\times \mathbf {A} f\mathbf {\nabla } \times \mathbf {A} }$

${\displaystyle \mathbf {\nabla } \times (\mathbf {A} \times \mathbf {B} )=(\mathbf {B} \cdot \mathbf {\nabla } )\mathbf {A} -(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} \mathbf {A} (\mathbf {\nabla } \cdot \mathbf {B} )-\mathbf {B} (\mathbf {\nabla } \cdot \mathbf {A} )}$

${\displaystyle \mathbf {\nabla } \times \mathbf {\nabla } f={\vec {0}}}$

${\displaystyle \mathbf {\nabla } \cdot (\mathbf {\nabla } \times \mathbf {A} )=0}$

${\displaystyle \mathbf {\nabla } \times (\mathbf {\nabla } \times \mathbf {A} )=\mathbf {\nabla } (\mathbf {\nabla } \cdot \mathbf {A} )-\mathbf {\nabla } ^{2}\mathbf {A} }$

ヘルムホルツ分解

${\displaystyle \mathbf {B} =\mathbf {\nabla } f \mathbf {\nabla } \times \mathbf {A} }$

積分公式

ここで ${\displaystyle \mathbf {A} }$, ${\displaystyle \mathbf {B} }$, ${\displaystyle \mathbf {C} }$ は任意のベクトル場, ${\displaystyle f}$, ${\displaystyle g}$ は任意のスカラー場である。また, ${\displaystyle V}$ は空間領域, ${\displaystyle \partial V}$ はその境界, ${\displaystyle S}$ は面, ${\displaystyle \mathbf {n} }$ はその法線ベクトル (${\displaystyle S=\partial V}$ の場合 ${\displaystyle \mathbf {n} }$ は外向きに取る), ${\displaystyle d\mathbf {S} =\mathbf {n} dS}$ は面要素ベクトルである。閉曲線 ${\displaystyle \partial S}$ に関する線積分 ${\displaystyle d\mathbf {r} }$ は法線 ${\displaystyle \mathbf {n} }$ に対応する向きとする。

ガウスの発散定理および関連する公式（最後の等式はグリーンの定理である）

${\displaystyle \int _{V}\mathbf {\nabla } \cdot \mathbf {A} \,dV=\oint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }$

${\displaystyle \int _{V}\mathbf {\nabla } f\,dV=\oint _{\partial V}f\,d\mathbf {S} }$

${\displaystyle \int _{V}\mathbf {\nabla } \times \mathbf {A} \,dV=\oint _{\partial V}d\mathbf {S} \times \mathbf {A} }$

${\displaystyle \int _{V}(f\mathbf {\nabla } ^{2}g-g\mathbf {\nabla } ^{2}f)dV=\oint _{\partial V}(f\mathbf {\nabla } g-g\mathbf {\nabla } f)\cdot d\mathbf {S} }$

ストークスの定理および関連する公式

${\displaystyle \int _{S}(\mathbf {\nabla } \times \mathbf {A} )\cdot d\mathbf {S} =\oint _{\partial S}\mathbf {A} \cdot d\mathbf {r} }$

${\displaystyle \int _{S}d\mathbf {S} \times \mathbf {\nabla } f=\oint _{\partial S}fd\mathbf {r} }$

${\displaystyle \int _{S}(d\mathbf {S} \times \mathbf {\nabla } )\times \mathbf {A} =\oint _{\partial S}d\mathbf {r} \times \mathbf {A} }$

曲線座標

曲線座標における勾配、発散、回転、ラプラシアン、物質微分の公式。

円柱座標

円柱座標 ${\displaystyle (r,\theta ,z)}$ と直交座標 ${\displaystyle (x,y,z)}$ の変換

${\displaystyle \left\{{\begin{array}{l}x=r\cos \theta \\y=r\sin \theta \\z=z\end{array}}\right.\ \ \ \ \left\{{\begin{array}{l}r={\sqrt {x^{2} y^{2}}}\\\theta =\tan ^{-1}{\frac {y}{x}}\\z=z\end{array}}\right.}$

単位基底ベクトル

${\displaystyle \mathbf {e} _{r}=\cos \theta \mathbf {e} _{x} \sin \theta \mathbf {e} _{y}}$

${\displaystyle \mathbf {e} _{\theta }=-\sin \theta \mathbf {e} _{x} \cos \theta \mathbf {e} _{y}}$

${\displaystyle \mathbf {e} _{z}=\mathbf {e} _{z}}$

計量

${\displaystyle ds^{2}=dr^{2} r^{2}d\theta ^{2} dz^{2}}$

体積要素

${\displaystyle dV=r\,dr\,d\theta \,dz}$

勾配

${\displaystyle \mathbf {\nabla } f={\frac {\partial f}{\partial r}}\mathbf {e} _{r} {\frac {1}{r}}{\frac {\partial f}{\partial \theta }}\mathbf {e} _{\theta } {\frac {\partial f}{\partial z}}\mathbf {e} _{z}}$

発散

${\displaystyle \mathbf {\nabla } \cdot \mathbf {A} ={\frac {1}{r}}{\frac {\partial }{\partial r}}(rA_{r}) {\frac {1}{r}}{\frac {\partial A_{\theta }}{\partial \theta }} {\frac {\partial A_{z}}{\partial z}}}$

回転

${\displaystyle \mathbf {\nabla } \times \mathbf {A} =\left({\frac {1}{r}}{\frac {\partial A_{z}}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial z}}\right)\mathbf {e} _{r} \left({\frac {\partial A_{r}}{\partial z}}-{\frac {\partial A_{z}}{\partial r}}\right)\mathbf {e} _{\theta } \left[{\frac {1}{r}}{\frac {\partial }{\partial r}}(rA_{\theta })-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\right]\mathbf {e} _{z}}$

ラプラシアン (スカラー場)

${\displaystyle \mathbf {\nabla } ^{2}f={\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial f}{\partial r}}\right) {\frac {1}{r^{2}}}{\frac {\partial ^{2}f}{\partial \theta ^{2}}} {\frac {\partial ^{2}f}{\partial z^{2}}}}$

ラプラシアン (ベクトル場)

${\displaystyle [\mathbf {\nabla } ^{2}\mathbf {A} ]_{r}=\mathbf {\nabla } ^{2}A_{r}-{\frac {2}{r^{2}}}{\frac {\partial A_{\theta }}{\partial \theta }}-{\frac {A_{r}}{r^{2}}}}$

${\displaystyle [\mathbf {\nabla } ^{2}\mathbf {A} ]_{\theta }=\mathbf {\nabla } ^{2}A_{\theta } {\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {A_{\theta }}{r^{2}}}}$

${\displaystyle [\mathbf {\nabla } ^{2}\mathbf {A} ]_{z}=\mathbf {\nabla } ^{2}A_{z}}$

物質微分

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{r}=(\mathbf {A} \cdot \mathbf {\nabla } )B_{r}-{\frac {A_{\theta }B_{\theta }}{r}}}$

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{\theta }=(\mathbf {A} \cdot \mathbf {\nabla } )B_{\theta } {\frac {A_{\theta }B_{r}}{r}}}$

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{z}=(\mathbf {A} \cdot \mathbf {\nabla } )B_{z}}$

球座標

球座標 ${\displaystyle (r,\theta ,\phi )}$ と直交座標 ${\displaystyle (x,y,z)}$ の変換

${\displaystyle \left\{{\begin{array}{l}x=r\sin \theta \cos \phi \\y=r\sin \theta \sin \phi \\z=r\cos \theta \end{array}}\right.\ \ \ \ \left\{{\begin{array}{l}r={\sqrt {x^{2} y^{2} z^{2}}}\\\theta =\cos ^{-1}{\frac {z}{r}}\\\phi =\tan ^{-1}{\frac {y}{x}}\end{array}}\right.}$

単位基底ベクトル

${\displaystyle \mathbf {e} _{r}=\sin \theta \cos \phi \mathbf {e} _{x} \sin \theta \sin \phi \mathbf {e} _{y} \cos \theta \mathbf {e} _{z}}$

${\displaystyle \mathbf {e} _{\theta }=\cos \theta \cos \phi \mathbf {e} _{x} \cos \theta \sin \phi \mathbf {e} _{y}-\sin \theta \mathbf {e} _{z}}$

${\displaystyle \mathbf {e} _{\phi }=-\sin \phi \mathbf {e} _{x} \cos \phi \mathbf {e} _{y}}$

計量

${\displaystyle ds^{2}=dr^{2} r^{2}(d\theta ^{2} \sin ^{2}\theta d\phi ^{2})}$

体積要素

${\displaystyle dV=r^{2}\sin \theta \,dr\,d\theta \,d\phi }$

勾配

${\displaystyle \mathbf {\nabla } f={\frac {\partial f}{\partial r}}\mathbf {e} _{r} {\frac {1}{r}}{\frac {\partial f}{\partial \theta }}\mathbf {e} _{\theta } {\frac {1}{r\sin \theta }}{\frac {\partial f}{\partial \phi }}\mathbf {e} _{\phi }}$

発散

${\displaystyle \mathbf {\nabla } \cdot \mathbf {A} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}A_{r}) {\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta A_{\theta }) {\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}}$

回転

${\displaystyle \mathbf {\nabla } \times \mathbf {A} ={\frac {1}{r\sin \theta }}\left[{\frac {\partial }{\partial \theta }}(\sin \theta A_{\phi })-{\frac {\partial A_{\theta }}{\partial \phi }}\right]\mathbf {e} _{r} {\frac {1}{r}}\left[{\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial }{\partial r}}(rA_{\phi })\right]\mathbf {e} _{\theta } {\frac {1}{r}}\left[{\frac {\partial }{\partial r}}(rA_{\theta })-{\frac {\partial A_{r}}{\partial \theta }}\right]\mathbf {e} _{\phi }}$

ラプラシアン (スカラー場)

${\displaystyle \mathbf {\nabla } ^{2}f={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial f}{\partial r}}\right) {\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial f}{\partial \theta }}\right) {\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}f}{\partial \phi ^{2}}}}$

ラプラシアン (ベクトル場)

${\displaystyle [\mathbf {\nabla } ^{2}\mathbf {A} ]_{r}=\mathbf {\nabla } ^{2}A_{r}-{\frac {2}{r^{2}}}{\frac {\partial A_{\theta }}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}-{\frac {2A_{r}}{r^{2}}}-{\frac {2\cot \theta A_{\theta }}{r^{2}}}}$

${\displaystyle [\mathbf {\nabla } ^{2}\mathbf {A} ]_{\theta }=\mathbf {\nabla } ^{2}A_{\theta } {\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cot \theta }{r^{2}\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}}$

${\displaystyle [\mathbf {\nabla } ^{2}\mathbf {A} ]_{\phi }=\mathbf {\nabla } ^{2}A_{\phi } {\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }} {\frac {2\cot \theta }{r^{2}\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}-{\frac {A_{\phi }}{r^{2}\sin ^{2}\theta }}}$

物質微分

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{r}=(\mathbf {A} \cdot \mathbf {\nabla } )B_{r}-{\frac {A_{\theta }B_{\theta } A_{\phi }B_{\phi }}{r}}}$

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{\theta }=(\mathbf {A} \cdot \mathbf {\nabla } )B_{\theta } {\frac {A_{\theta }B_{r}}{r}}-{\frac {A_{\phi }B_{\phi }\cot \theta }{r}}}$

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{\phi }=(\mathbf {A} \cdot \mathbf {\nabla } )B_{z} {\frac {A_{\phi }B_{r}}{r}} {\frac {A_{\phi }B_{\theta }\cot \theta }{r}}}$

直交曲線座標

3次元ユークリッド空間 ${\displaystyle \mathbb {R} ^{3}}$ の曲線座標 ${\displaystyle x^{i}}$ について、その座標系で計量が

${\displaystyle ds^{2}=\sum _{i=1}^{3}h_{i}(x)^{2}(dx^{i})^{2}}$

という対角形になるとき、これを直交曲線座標と呼ぶ。この座標系に付随する規格化された基底ベクトルを ${\displaystyle \mathbf {e} _{i}}$ とする。

体積要素

${\displaystyle dV=hdx^{1}dx^{2}dx^{3},\ \ h=h_{1}h_{2}h_{3}}$

勾配

${\displaystyle \mathbf {\nabla } f=\sum _{i=1}^{3}{\frac {1}{h_{i}}}{\frac {\partial f}{\partial x^{i}}}\mathbf {e} _{i}}$

発散

${\displaystyle \mathbf {\nabla } \cdot \mathbf {A} =\sum _{i=1}^{3}{\frac {1}{h}}{\frac {\partial }{\partial x^{i}}}\left({\frac {h}{h_{i}}}A_{i}\right)}$

回転

${\displaystyle \mathbf {\nabla } \times \mathbf {A} =\sum _{i=1}^{3}\mathbf {e} _{i}\sum _{j=1}^{3}\sum _{k=1}^{3}\epsilon _{ijk}{\frac {h_{i}}{h}}{\frac {\partial (h_{k}A_{k})}{\partial x^{j}}}}$

ラプラシアン (スカラー場)

${\displaystyle \mathbf {\nabla } ^{2}f=\sum _{i=1}^{3}{\frac {1}{h}}{\frac {\partial }{\partial x^{i}}}\left({\frac {h}{h_{i}^{2}}}{\frac {\partial f}{\partial x^{i}}}\right)}$

物質微分

${\displaystyle [(\mathbf {A} \cdot \mathbf {\nabla } )\mathbf {B} ]_{i}=\sum _{k=1}^{3}\left[{\frac {A_{k}}{h_{k}}}{\frac {\partial B_{i}}{\partial x_{k}}} \left(A_{i}{\frac {\partial h_{i}}{\partial x_{k}}}-A_{k}{\frac {\partial h_{k}}{\partial x_{i}}}\right){\frac {B_{k}}{h_{k}h_{i}}}\right]}$

脚注
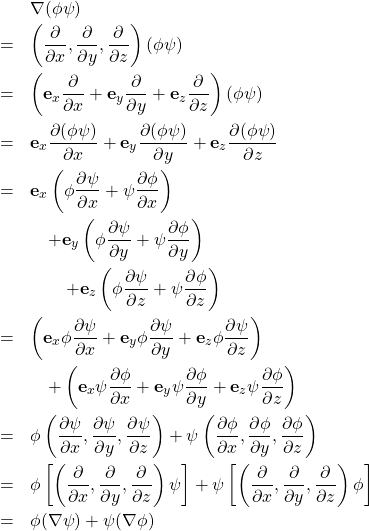