切断正規分布

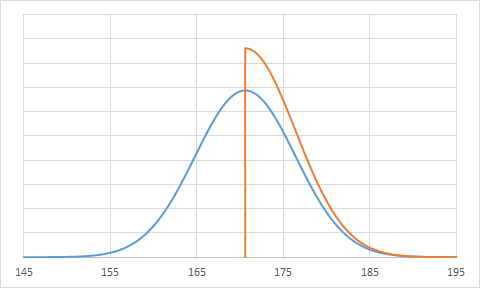
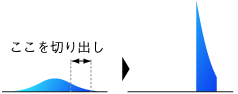
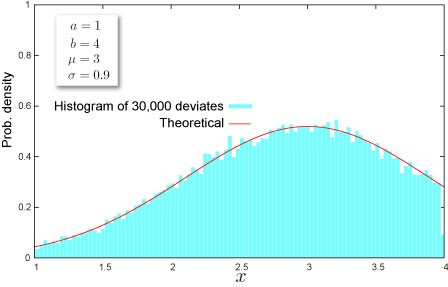
切断正規分布 (せつだんせいきぶんぷ) は正規分布と似ているが、確率変数 ${\displaystyle x}$ の定義域が有限な確率分布である。上下とも有界 (A ≤ x ≤ B) なものを二重に切断された正規分布、どちらか一方だけのものを単一切断正規分布という。

定義と性質

切断正規分布の確率密度関数は以下で定義される。

${\displaystyle f(x;\mu ,\sigma ,a,b)={\frac {{\frac {1}{\sigma }}\phi ({\frac {x-\mu }{\sigma }})}{\Phi ({\frac {b-\mu }{\sigma }})-\Phi ({\frac {a-\mu }{\sigma }})}}}$

ここで ${\displaystyle \scriptstyle {\phi (\cdot )}\ }$ は標準正規分布 N(0, 1) の確率密度関数、 ${\displaystyle \scriptstyle {\Phi (\cdot )}}$ は標準正規分布 N(0, 1) の累積分布関数である。

モーメント

切断正規分布の期待値と分散は、二重に切断されている場合、

${\displaystyle \operatorname {E} (X|A$

${\displaystyle \operatorname {Var} (X|A$

であり、単一切断正規分布の場合は

${\displaystyle \operatorname {E} (X|X>A)=\mu {\frac {\sigma }{R\left({\frac {A-\mu }{\sigma }}\right)}}}$

${\displaystyle \operatorname {Var} (X|X>A)=\sigma ^{2}\left[1 {\frac {\frac {A-\mu }{\sigma }}{R\left({\frac {A-\mu }{\sigma }}\right)}}-\left\{{\frac {1}{R\left({\frac {A-\mu }{\sigma }}\right)}}\right\}^{2}\right]}$

である。ここで

${\displaystyle R\left({\frac {x-\mu }{\sigma }}\right)={\frac {1-\Phi \left({\frac {x-\mu }{\sigma }}\right)}{\phi \left({\frac {x-\mu }{\sigma }}\right)}}}$

は、ミルズ比である。

参考文献

• 蓑谷千凰彦、統計分布ハンドブック、朝倉書店 (2003).

関連項目

• 確率分布